¿Como funciona Shazam en su esplendor? Aquí se lo explicamos.
Hola muy buenas a todos bienvenidos a otro post más de este maravilloso
blog TecnologiasRapida, este post no va dedicado a ningún aficionado a un Sistema
operativo si no que va destinado a todas esas personas curiosas que le interesa
saber como funcionan las aplicaciones como shazam o como siri o el asistente de
google es capaz de reconocer las canciones.
Oyes una canción familiar en el club o en el restaurante. Has escuchado
esta canción miles de veces desde hace mucho tiempo y el sentimentalismo de la
canción realmente toca tu corazón. ¡Desesperadamente la quieres volver a
escuchar en la mañana, pero no recuerdas su nombre! Afortunadamente, en nuestro
increíble mundo futurista, tienes un teléfono con software de reconocimiento de música instalado. Puedes relajarte,
ya que el Software te dijo el nombre de la canción, así que sabes que la puedes
escuchar una y otra vez hasta que se convierta en una parte de ti…o te llegue a
desesperar…
Mobile technologies, junto con el progreso del procesamiento de la señal de audio, nos han
dado, algorithm developers, la habilidad de crear reconocedores de música., la
aplicación creará una huella digital de la muestra grabada, consultará la base
de datos, y utilizará su algoritmo de reconocimiento de música para decirte
exactamente cual es la canción que estás escuchando.
¿Como funciona Shazam realmente? Shazam’s algorithm La
aplicación fue expuesta por primera vez por su inventor Avery Li-Chung Wang en
el 2003. En este artículo hablaremos de los fundamentos del algoritmo de
reconocimiento de música Shazam.
Capturando el sonido (Grabando)
Grabar una señal de audio muestreado es fácil. Ya que las tarjetas de
sonido modernas ya vienen con convertidores analógicos-digitales, sólo tienes
que seleccionar un lenguaje de programación, encontrar una biblioteca adecuada
y establecer la frecuencia de la muestra, el número de canales (mono o estéreo)
y normalmente, el tamaño de la muestra (por ej. Muestras de 16 bits). Después
abre la línea de tu tarjeta de sonido, al igual que cualquier flujo de entrada,
y escribe en una matriz de bytes. Así es cómo puedes hacerla en Java:
private AudioFormat getFormat() {
float sampleRate = 44100;
int sampleSizeInBits = 16;
int channels = 1; //mono
boolean signed = true; //Indicates whether the data is signed or unsigned
boolean bigEndian = true; //Indicates whether the audio data is stored in big-endian or little-endian order
return new AudioFormat(sampleRate, sampleSizeInBits, channels, signed, bigEndian);
}
final AudioFormat format = getFormat(); //Fill AudioFormat with the settings
DataLine.Info info = new DataLine.Info(TargetDataLine.class, format);
final TargetDataLine line = (TargetDataLine) AudioSystem.getLine(info);
line.open(format);
line.start();
Lee los datos de ‘TargetDataLine’:
OutputStream out = new ByteArrayOutputStream();
running = true;
try {
while (running) {
int count = line.read(buffer, 0, buffer.length);
if (count > 0) {
out.write(buffer, 0, count);
}
}
out.close();
} catch (IOException e) {
System.err.println("I/O problems: " + e);
System.exit(-1);
}Dominio de tiempo y frecuencias
Lo que tenemos en esta matriz de bytes es la
señal grabada en el tiempo del dominio. La señal de dominio de tiempo
representa el cambio de amplitud de la señal a lo largo del tiempo.
Es posible representar cualquier señal en el
dominio del tiempo simplemente dando el conjunto de frecuencias, amplitudes y
fases correspondientes a cada sinusoide que compone la señal. Esta
representación de la señal es conocida como la frecuencia de dominio. En cierto
modo, el dominio de la frecuencia actúa como un tipo de huella dactilar o firma
para la señal de dominio de tiempo, proporcionando una representación estática
de una señal dinámica.
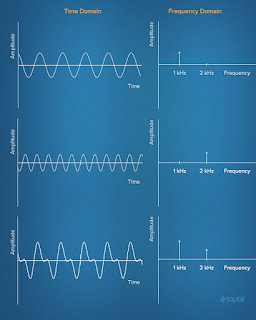
La siguiente foto muestra la serie de Fourier de
una onda cuadrada de 1 HZ y cómo
una onda cuadrada (aproximada) puede ser generada a partir de componentes
sinusoidales. La señal se muestra en el dominio del tiempo anterior y en el
dominio de la frecuencia a continuación
Analizar una señal en el dominio de la frecuencia simplifica muchas cosas
inmensamente. Después de eso, uno puede hacer el filtrado, aumentar o disminuir
algunas frecuencias, o simplemente reconocer el tono exacto de las frecuencias.
Transformación de Fourier
Por lo tanto, necesitamos encontrar una
manera de convertir nuestra señal desde el momento de dominio para el dominio
de la frecuencia. Aquí lo llamamos la transformación discreta de Fourie (DFT) para ayudar. La DFT es un
método matemático para realizar analisis
de Fourie en una muestra de la
señal. Convierte una lista finita de muestras equidistantes de una función en
la lista de los coeficientes de una combinación finita de complejas sinusoides,
ordenadas por sus frecuencias, considerando si las sinusoides habían sido
muestreadas en la misma proporción.
Uno de los algoritmos numéricos más
populares para el cálculo de la DFT es la Fast
Fourier Transform (FFT). El más
utilizado es la variación de FFT Cooley–Tukey algorithm.
Este algoritmo es del tipo divide-y-vencerás que recursivamente divide una DFT
en varias y pequeñas DFTs. Mientras que la evaluación de un DFT requiere
directamente O(n2) operations, with a Cooley-Tukey FFT el mismo se computa en
iO(n log n) operations.
No es difícil encontrar una biblioteca adecuada para la FFT. Aquí están
algunos de ellos:
·C – FFTW
·C++ – EigenFFT
·Java – JTransform
·Python – NumPy
·Ruby – Ruby-FFTW3 (Interface to FFTW)
A continuación se muestra un ejemplo de una
función FFT escrita en Java:
public static Complex[] fft(Complex[] x) {
int N = x.length;
// fft of even terms
Complex[] even = new Complex[N / 2];
for (int k = 0; k < N / 2; k++) {
even[k] = x[2 * k];
}
Complex[] q = fft(even);
// fft of odd terms
Complex[] odd = even; // reuse the array
for (int k = 0; k < N / 2; k++) {
odd[k] = x[2 * k + 1];
}
Complex[] r = fft(odd);
// combine
Complex[] y = new Complex[N];
for (int k = 0; k < N / 2; k++) {
double kth = -2 * k * Math.PI / N;
Complex wk = new Complex(Math.cos(kth), Math.sin(kth));
y[k] = q[k].plus(wk.times(r[k]));
y[k + N / 2] = q[k].minus(wk.times(r[k]));
}
return y;
}
Y aquí está un ejemplo de una señal antes y después del análisis FFT:
Huellas digitales en una canción
Un desafortunado efecto colateral de FFT es que perdemos una gran
cantidad de información acerca de la sincronización para una canción de 3
minutos, es por eso que introducimos el tipo de ventana deslizante, o fragmento
de datos así como la transformación de esta parte de la información. El tamaño
de cada fragmento puede determinarse de distintas formas. Por ejemplo, si
queremos grabar el sonido en estéreo, con muestras de 16 bits, a 44.100 Hz, un
segundo de ese sonido será de 44.100 muestras * 2 bytes * 2 canales ≈ 176 kB.
Si cogemos 4 kB para el tamaño de un segmento, tendremos 44 porciones de datos
para analizar en cada segundo de la canción. Esa es una buena densidad
suficiente para el análisis detallado.
Ahora volvamos a la programación:
byte audio [] = out.toByteArray()
int totalSize = audio.length
int sampledChunkSize = totalSize/chunkSize;
Complex[][] result = ComplexMatrix[sampledChunkSize][];
for(int j = 0;i < sampledChunkSize; j++) {
Complex[chunkSize] complexArray;
for(int i = 0; i < chunkSize; i++) {
complexArray[i] = Complex(audio[(j*chunkSize)+i], 0);
}
result[j] = FFT.fft(complexArray);
}
Vamos a formar nuestra huella digital de la
canción. Esta es la parte más importante de todo el proceso de reconocimiento
de música de Shazam. El principal desafío es cómo distinguir, en el océano de
las frecuencias capturadas, las frecuencias que son las más importantes.
Intuitivamente, podemos buscar las frecuencias con mayor magnitud.
Sin embargo, en una canción de la gama de
frecuencias fuerte puede variar entre baja C - C1 (32,70 Hz) y alta C - C8
(4,186.01 Hz). Así que en lugar de analizar toda la gama de frecuencias a la
vez, podemos elegir varios intervalos más pequeños. Elige en base a las
frecuencias comunes de componentes musicales importantes y analiza cada uno por
separado. Por ejemplo, estos son los 30 Hz - 40 Hz, 40 Hz - 80 Hz y 80 Hz - 120
Hz para los tonos bajos (cubriendo bass guitar, por ejemplo), y 120 Hz - 180 Hz
y 180 Hz - 300 Hz para el oriente y los tonos más altos (que cubre la mayoría
de los demás instrumentos y voces).
Ahora, dentro de cada intervalo podemos determinar la frecuencia con la
mayor magnitud. Esta información constituye una firma para esta parte de la
canción y esta firma se convierte en parte de la huella digital de la canción
como un todo.
public final int[] RANGE = new int[] { 40, 80, 120, 180, 300 };
// find out in which range is frequency
public int getIndex(int freq) {
int i = 0;
while (RANGE[i] < freq)
i++;
return i;
}
// result is complex matrix obtained in previous step
for (int t = 0; t < result.length; t++) {
for (int freq = 40; freq < 300 ; freq++) {
// Get the magnitude:
double mag = Math.log(results[t][freq].abs() + 1);
// Find out which range we are in:
int index = getIndex(freq);
// Save the highest magnitude and corresponding frequency:
if (mag > highscores[t][index]) {
points[t][index] = freq;
}
}
// form hash tag
long h = hash(points[t][0], points[t][1], points[t][2], points[t][3]);
}
private static final int FUZ_FACTOR = 2;
private long hash(long p1, long p2, long p3, long p4) {
return (p4 - (p4 % FUZ_FACTOR)) * 100000000 + (p3 - (p3 % FUZ_FACTOR))
* 100000 + (p2 - (p2 % FUZ_FACTOR)) * 100
+ (p1 - (p1 % FUZ_FACTOR));
}
Debemos incluir un factor de
aproximación ya que esto no esta echo a la perfección. Un análisis del factor
de aproximación debe ser tomado en serio y en un sistema real, el programa debe
tener una opción para establecer este parámetro en función a las condiciones de
la grabación.
Para facilitar la búsqueda, esta firma se convierte en la clave en una
tabla de hashtag. El valor correspondiente es el tiempo en el que este conjunto
de frecuencias apareció en la canción, junto con el ID de la canción (título de
la canción y del artista). Aquí está un ejemplo de cómo pueden aparecer estos
registros en la base de datos.
Si ejecutamos toda una biblioteca de canciones a
través de este proceso, podemos construir una base de datos completa con una
huella digital de cada canción en la biblioteca.
Elegir una canción
Como sucede, muchos de los hashtags corresponden a varias canciones. Por
ejemplo, puede ser que alguna pieza de una canción suena exactamente como algún
fragmento de canción E. Por supuesto, esto no es sorprendente – los músicos
siempre han “prestado” letras de canciones unos de otros y, en estos días, los
productores muestran otras canciones todo el tiempo. Cada vez que hemos partido
de un hashtag, el número de coincidencias posibles se hace más pequeño, pero es
probable que esta información por sí sola no va a reducir el partido a una sola
canción. Así que hay una cosa más que tenemos que verificar con nuestro
algoritmo de reconocimiento de música, y esa es la distribución
// Class that represents specific moment in a song
private class DataPoint {
private int time;
private int songId;
public DataPoint(int songId, int time) {
this.songId = songId;
this.time = time;
}
public int getTime() {
return time;
}
public int getSongId() {
return songId;
}
}
La grabación seguro que incluye un montón de ruido que introducirá
algunos errores en los partidos. Así que en lugar de tratar de eliminar todo
pero la canción correcta de nuestra lista de partidos, al final, hemos
conciliado ordenar todas las canciones en orden descendente de probabilidad, y
nuestra favorita es la primera canción en la lista de clasificación.
Conclusión y ultimo punto
Este tipo de software de reconocimiento de música
puede ser utilizado para encontrar las similitudes entre las canciones. Ahora
que entiendes cómo funciona Shazam, puedes ver cómo esto puede tener
aplicaciones más allá de la simple Shazaming que esa nostálgica canción que
suena en la radio del taxi. Y para acabar les dejo un imagen donde se resume el proceso.
Y bueno hasta aquí todo espero que les halla gustado este artículo tan interesante y sobre todo el ultimo de este año, les deseo muy buen feliz año nuevo y espero que disfruten esta noche, y no os paséis con el alcohol eeee pillines😉😊
Y por ultimo darle las gracias a Toptal por cerrar el año conmigo y seguir confiando en mi.
Si les ha gustado compartanlo denle a
seguir y dejen sus comentarios ya que nos ayudan a crecer más y saber si lo
hacemos bien o no. Hasta Luegoo people...
Twitter:
@tecnologiasrapi
Enlace del post:https://www.toptal.com/algorithms/shazam-reconocimiento-de-algoritmos-de-m%C3%BAsica-huellas-dactilares-y-procesamiento/es
Instagram/Snapchat:rubenvrodriguez
Contacto en: rubenvargasrodriguez4@gmail.com







Comentarios
Publicar un comentario